
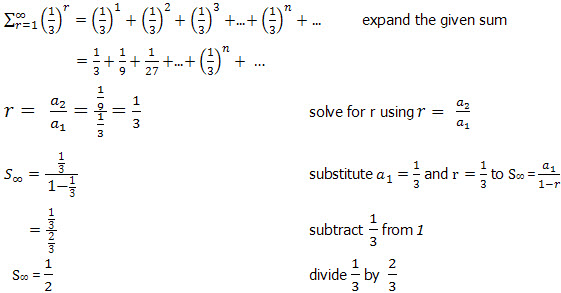
Mathematicians also refer to generic sequences using the letter a along with subscripts that correspond to the term numbers as follows: Mathematicians use the letter r when referring to these types of sequences. So that we can examine these sequences to greater depth, we must know that the fixed numbers that bind each sequence together are called common ratios. The fourth number times -1/2 is the fifth number: -2 × -1/2 = 1.īecause these sequences behave according to this simple rule of multiplying a constant number to one term to get to another, they are called geometric sequences. This too works for any pair of consecutive numbers. We need to multiply by -1/2 to the first number to get the second number. Sequence C is a little different because it seems that we are dividing yet to stay consistent with the theme of geometric sequences, we must think in terms of multiplication. The third number times 6 is the fourth number: 0.36 × 6 = 2.16, which will work throughout the entire sequence. This also works for any pair of consecutive numbers. The second number times 2 is the third number: 2 × 2 = 4, and so on.įor sequence B, if we multiply by 6 to the first number we will get the second number. This works for any pair of consecutive numbers. įor sequence A, if we multiply by 2 to the first number we will get the second number. The following sequences are geometric sequences: Note that n will be 6 in our formula since our series is set up to go from n = 1 to n = 6.Sequences of numbers that follow a pattern of multiplying a fixed number from one term to the next are called geometric sequences. Sample Problemįormula to the rescue…again. But that's kind of expected since this series would be considered a divergent infinite geometric series and, as a result, has some seriously big partial sums along the way. We can also put in 5 for n since we're asked to find the fifth partial sum. Let's take the partial sum formula and substitute a 1 = 2 and r = 3. We're multiplying each term by 3, so our common ratio is 3. Sample Problemįind the fifth partial sum of the geometric series: Even though we're adding an infinite number of terms, their sum will get closer and closer to 6. We'll use our formula and then get on with our lives. This one's a convergent series with a first term of a 1 = 3 and a common ratio of r = ½. Sample Problemįind the sum of the infinite geometric series given by. That means the series diverges and its sum is infinitely large. In fact, we can tell if an infinite geometric series converges based simply on the value of r. While the ideas of convergence and divergence are a little more involved than this, for now, this working knowledge will do. This is only the 21st term of this series, but it's very small.

This is especially true when we add in terms like. However, each time we add in another term, the sum is not going to get that much bigger. On the other hand, the series with the terms has a sum that also increases with each additional term. This series is divergent, not convergent. We can see that each time we add in another number, the sum is going to get larger and larger and larger and larger and larger and larger…you get the idea. does not converge because every time we put another number into our sum, the sum gets a lot bigger. The series with the terms 1, 2, 4, 8, 16, 32. A convergent series is one whose partial sums get closer to a certain value as the number of terms increases. Unfortunately, and this is a big "unfortunately," this formula will only work when we have what's known as a convergent geometric series. All we need is the first term and the common ratio and boom-we have the sum.

This formula really couldn't be much simpler.

The first is the formula for the sum of an infinite geometric series. We'll do both cool your jets.īefore we jump into sample problems, we'll need two formulas to find these sums. Not only can we find partial sums like we did with arithmetic sequences, we can find the overall sum as well. In this series, our numbers will start when n = 1 and go all the way to infinity. We use the same sigma notation we used with arithmetic series, so we have a general form that looks like this: Instead of just listing all the terms with commas in between, we take the sum of everything. A geometric series is just the added-together version of a geometric sequence.


 0 kommentar(er)
0 kommentar(er)
